Getting started with CoDaImpact

Introduction

CoDaImpact is a package for the analysis of covariate impacts in compositional regression models. It is designed to work in conjunction with the compositions package. The compositions package is used to fit a regression model involving compositional variables and the CoDaImpact package provides new functions to interpret the estimation results.

The interface between the two packages is implemented by the CoDaImpact::ToSimplex() function which converts the usual lm object into an object of class lmCoDa. This new class is associated with new interpretation methods that make use of elasticities and semi-elasticities (see Morais and Thomas-Agnan, 2021) and share ratio elasticities (see Dargel and Thomas-Agnan, 2024). A finite increments interpretation is also provided in the function CoDaImpact::VariationTable(). Finally, some visualization tools are provided.

The Dargel and Thomas-Agnan (2024) paper is illustrated by vignette and all materials for reproducing the results in the paper and the vignette can be found on a dedicated GitHub repository.

The following three sections illustrate the use of the CoDaImpact package for three classes of regression models:

scalar on composition case: the response is scalar and at least one of the explanatory variables is a composition,
composition on scalar case: the response is a composition and the explanatory variables are scalar,
composition on composition case: the response is a composition and at least one of the explanatory variables is a composition.

<! – Section 4 provides implementation details. –> <! – The package contains three data sets used as examples: rice_yields, car_market, elections. –>

The following code loads all the packages required for this vignette. The CoDaImpact package has to be installed from GitHub for now and should be released on CRAN later on.

# remotes::install_github("LukeCe/CoDaImpact")
library(CoDaImpact)
library(compositions)

Scalar on composition regression

This case is illustrated using an example from Trinh et al. (2023) studying the impact of climate change on rice yield in Vietnam.

Rice yield data

The rice_yields dataset contains the rice production “YIELD” in each province of Vietnam, between 1987 and 2016. The data on rice yields originate from “International Rice Research Institute”. The maximum daily temperature data originate from the database “Climate Prediction Center (CPC)”, created by “National Oceanic and Atmospheric Administration (NOAA)”. The temperatures have been interpolated over the 63 provinces using areal interpolation methods. For this illustration, we group the temperatures in three classes LOW ([-6,25.1]), MEDIUM ([25.1,35.4]) and HIGH ([35.4,45]). The precipitation data come from the project “Asian Precipitation-Highly-Resolved Observational Data Integration Towards Evaluation (APHRODITE)”.

summary(rice_yields)

##           PROVINCE                                        REGION   
##  ANGIANG      :  30   Central Highlands                      :180  
##  BACGIANG     :  30   Mekong Delta                           :420  
##  BACKAN       :  30   Midlands and Northern Mountainous Areas:390  
##  BACLIEU      :  30   Northern and Coastal Central Region    :420  
##  BACNINH      :  30   Red River Delta                        :330  
##  BARIA-VUNGTAU:  30   Southeastern Area                      :150  
##  (Other)      :1710                                                
##       YEAR          YIELD       PRECIPITATION   
##  Min.   :1987   Min.   :1.120   Min.   :0.1693  
##  1st Qu.:1994   1st Qu.:3.094   1st Qu.:1.1656  
##  Median :2002   Median :4.096   Median :1.4040  
##  Mean   :2002   Mean   :4.077   Mean   :1.3824  
##  3rd Qu.:2009   3rd Qu.:5.027   3rd Qu.:1.6411  
##  Max.   :2016   Max.   :6.637   Max.   :3.7032  
##                                                 
##    TEMPERATURES.LOW    TEMPERATURES.MEDIUM    TEMPERATURES.HIGH  
##  Min.   :0.0000003     Min.   :0.5150684     Min.   :0.00000020  
##  1st Qu.:0.0027399     1st Qu.:0.6438356     1st Qu.:0.00273983  
##  Median :0.1945206     Median :0.7657533     Median :0.02185802  
##  Mean   :0.1704263     Mean   :0.7957867     Mean   :0.03378702  
##  3rd Qu.:0.3095891     3rd Qu.:0.9726024     3rd Qu.:0.05205488  
##  Max.   :0.4699453     Max.   :0.9999995     Max.   :0.25479457  
##

The following plot is a ternary diagram of maximum temperature colored according to rice yield.

whitered_pal <- colorRampPalette(rev(c("beige","orange","red","darkred")))

top100 <- head(rice_yields, 250)
whitered_col <- whitered_pal(length(top_100$YIELD))

## Error in eval(expr, envir, enclos): object 'top_100' not found

yield_top100 <- rank(top_100$YIELD,ties.method = "first")

## Error in eval(expr, envir, enclos): object 'top_100' not found

ylcol_top100 <- whitered_col[yield_top100]

## Error in eval(expr, envir, enclos): object 'whitered_col' not found

layout(matrix(1:2,ncol=2), width = c(2,1),height = c(1,1))
plot(acomp(top_100$TEMPERATURES),
     col = ylcol_top100,
     pch = 16)

## Error in eval(expr, envir, enclos): object 'top_100' not found

legend_image <- as.raster(matrix(whitered_pal(20), ncol=1))
plot(c(0,2),c(0,1),type = 'n', axes = F,xlab = '', ylab = '', main = 'Rice yield')
yield_range <- range(top_100$YIELD)

## Error in eval(expr, envir, enclos): object 'top_100' not found

yield_range <- seq(min(yield_range), max(yield_range), l = 5)

## Error in eval(expr, envir, enclos): object 'yield_range' not found

text(x=1.5, y = seq(0,1,l=5), labels = (round(yield_range,1)))

## Error in eval(expr, envir, enclos): object 'yield_range' not found

rasterImage(legend_image, 0, 0, 1,1)

Regression step with the compositions package

This model explains a scalar variable YIELD with a combination of scalar and compositional variables. Before estimating, we have to store our data in a data.frame in such a way that scalar variables are column vectors and compositional variables are matrices. In our dataset, the TEMPERATURES variable is already in the matrix format.

sapply(rice_yields, class)

## $PROVINCE
## [1] "factor"
## 
## $REGION
## [1] "factor"
## 
## $YEAR
## [1] "numeric"
## 
## $YIELD
## [1] "numeric"
## 
## $PRECIPITATION
## [1] "numeric"
## 
## $TEMPERATURES
## [1] "matrix" "array"

rice_yields$TEMPERATURES[1,] #LOW, MEDIUM, and HIGH, are grouped in TEMPERATURES

##             LOW          MEDIUM            HIGH 
## 0.0000002999999 0.9616434547947 0.0383562452054

We continue to fit a regression model with the tools provided by base R and the compositions package, in particular, the lm() function and the alr() transformation for the TEMPERATURES variable.

fit_X_compo <- lm(YIELD ~ PRECIPITATION + alr(TEMPERATURES),data = rice_yields)
class(fit_X_compo)

## [1] "lm"

In the next step the function ToSimplex() transforms the above output into a “lmCoDa” class which serves as the interface between the lm-output and the interpretation functions.

fit_X_compo <- ToSimplex(fit_X_compo)
class(fit_X_compo)

## [1] "lmCoDa" "lm"

The same can be achieved in a single step using the lmCoDa() function.

fit_X_compo <- lmCoDa(YIELD ~ PRECIPITATION + alr(TEMPERATURES),data = rice_yields)
class(fit_X_compo)

## [1] "lmCoDa" "lm"

coef

The estimated parameters can be retrieved by the coef() function. For a compositional explanatory variable the option space allows choosing between the simplex version, the clr version or the coordinate version of the parameters.

coef(fit_X_compo,space = "simplex")

##                   YIELD
## (Intercept)   3.5835270
## PRECIPITATION 0.2528452
## LOW           0.3338069
## MEDIUM        0.3413303
## HIGH          0.3248628

coef(fit_X_compo,space = "clr")

##                      YIELD
## (Intercept)    3.583526963
## PRECIPITATION  0.252845153
## LOW            0.001623843
## MEDIUM         0.023911877
## HIGH          -0.025535720

coef(fit_X_compo) # by default use the log-ratio of the estimation, here alr

##                               YIELD
## (Intercept)             3.583526963
## PRECIPITATION           0.252845153
## alr(TEMPERATURES)LOW    0.001623843
## alr(TEMPERATURES)MEDIUM 0.023911877

fitted

The fitted() function retrieves the fitted values.

head(fitted(fit_X_compo))

##        1        2        3        4        5        6 
## 3.924848 3.736444 3.948922 4.013668 3.871424 3.952286

residuals

The function residuals() retrieves the residuals.

head(resid(fit_X_compo))

##          1          2          3          4          5          6 
## -0.5188733 -0.7565444 -1.6756716 -1.6125383 -1.2580224 -1.3394688

Interpretation tools

Finite increments interpretation

Finite increments interpretation as in Muller et al. (2018) can be obtained using outputs in coordinate space. For the case of scalar on composition regression, more interpretations are found in Coenders and Pawlovsky-Glahn (2020). The different formulations they propose correspond to different parametrizations of the model and we illustrate below their interpretation based on clr coordinates.

Interpretation with ilr coordinates

Using the approach of Muller et al. (2018) we interpret an additive increment for a specific ilr coordinate that corresponds to a so-called principal balance. To use their interpretation we first need to transform the parameters into the appropriate ilr space, which is defined by the contrast matrix. The ilrBase() function without further arguments leads to the principal balance of the last component against all others.

V_TEMP   <- ilrBase(D = 3)
V_TEMP

##         [,1]       [,2]
## 1 -0.7071068 -0.4082483
## 2  0.7071068 -0.4082483
## 3  0.0000000  0.8164966

We can use this contrast matrix and the parameters in clr space to obtain the ilr parameters.

clr_TEMP <- coef(fit_X_compo, space = "clr", split = TRUE)[["alr(TEMPERATURES)"]]
ilr_TEMP <- t(V_TEMP) %*% clr_TEMP
ilr_TEMP

##            YIELD
## [1,]  0.01576002
## [2,] -0.03127474

The interpretation is that an additive increment of one unit in the second ilr coordinate leads to an expected decrease in the rice yield by 0.03 tonnes per hectare. This increment means that the ratio between HIGH and the geometric mean of LOW and MEDIUM is approximately multiplied by \(\exp(1/0.82)\sim 3.44,\) where \(O.82\) is the element \((3,2)\) of the contrast matrix.

In terms of temperature distribution, the above increment implies that the third component HIGH of the temperature composition grows at the expense of the others (the geometric mean of the other two) in a way that the ratio of LOW to MEDIUM remains constant. This corresponds to a change in the TEMPERATURES simplex in the direction of the vertex HIGH. Changing for another vertex is simple by a permutation of the rows of the contrast matrix.

This method only allows to evaluate the impacts of changing a compositional covariate in the direction of a vertex. In Dargel and Thomas-Agnan (2024) it is shown how the impact of more general changes in explanatory compositions can be interpreted.

Interpretation with clr coordinates

The clr parameter estimates for the temperatures are given by:

clr_TEMP

##               YIELD
## LOW     0.001623843
## MEDIUM  0.023911877
## HIGH   -0.025535720

We follow Coenders and Pawlovsky-Glahn (2020) but without changing the base of the logarithm and the normalization constant. In these conditions, the first clr parameter for the level LOW of temperature is interpreted as the expected change of the response when the ratio between LOW and the geometric mean of LOW, MEDIUM and HIGH is multiplied by \(\exp(1)\sim 2.7\). The resulting change in expected yield is therefore an increase of \(0.0016\) tons per hectare.

Variation scenario in the simplex space

To evaluate the impact of a given compositional covariate, we create scenarios of changes in its simplex space described by a linear equation \(x(h)=x(0)\oplus h\odot u,\) where \(x(0)\) is the initial point, \(h\) is the signed-intensity of change and \(u\) is a vector of the simplex defining the direction of change. We then compute the predicted value of \(y(h)\) corresponding to \(x(h)\).

We consider a change in the direction of the vertex “LOW” of the variable “TEMPERATURE”, and we predict new values of the response variable according to the change in percentage points of this vertex.

VariationScenario(
  fit_X_compo,
  Xvar = "TEMPERATURES",
  Xdir = c(0.2, 0.5, 0.3),
  inc_size = 2,
  n_steps = 5,
  add_opposite = TRUE,
  obs=43)

##       YIELD           X.LOW        X.MEDIUM          X.HIGH
## -5 3.819922 0.9989636850642 0.0000018748701 0.0010344400657
## -4 3.855516 0.9963715150059 0.0000314423589 0.0035970426351
## -3 3.891110 0.9870530721012 0.0005237290466 0.0124231988521
## -2 3.926704 0.9498471187296 0.0084740730707 0.0416788081997
## -1 3.962298 0.7674684242080 0.1151254523609 0.1174061234311
## 0  3.997893 0.2465753931507 0.6219176838356 0.1315069230137
## 1  4.033487 0.0220905961112 0.9368346502406 0.0410747536483
## 2  4.069081 0.0013878377613 0.9896156353605 0.0089965268782
## 3  4.104675 0.0000832426310 0.9980354895354 0.0018812678336
## 4  4.140269 0.0000049585605 0.9996043543177 0.0003906871218
## 5  4.175863 0.0000002949985 0.9999186719961 0.0000810330054

For a good visual impression, it is better to use a smaller step size and a larger number of steps. Below is the ternary diagram showing the path in the simplex: the initial point is in black and the other ones are colored according to the value of rice yield.

VS2 <- VariationScenario(
  fit_X_compo,
  Xvar = "TEMPERATURES",
  Xdir = c(0.2, 0.5, 0.3),
  inc_size = .1,
  n_steps = 40,
  add_opposite = TRUE,
  obs=43)

yield_color <- whitered_pal(length(VS2$YIELD))
yield_color <- yield_color[rank(VS2$YIELD,ties.method = "first")]
plot(acomp(VS2$X), col = yield_color, pch = 16)
plot(acomp(VS2["0", "X"]), add = TRUE, pch = 16)

Infinitesimal increments interpretation

Semi-elasticities

The use of semi-elasticities for the interpretation of compositional covariates is described in Morais and Thomas-Agnan (2021). For a scalar on composition model the Impacts() method computes the semi-elasticities for all compositional covariates.

RY_Impacts <- Impacts(fit_X_compo, Xvar = "TEMPERATURES")
RY_Impacts # here, the semi-elasticity is computed for the variable TEMPERATURES

##               YIELD
## LOW     0.001623843
## MEDIUM  0.023911877
## HIGH   -0.025535720

Increments approach

Dargel and Thomas-Agnan (2024) use semi-elasticities to interpret infinitesimal changes due to variation scenarios. The function VariationTable computes the impact of incremental changes in covariates on the response variable. The covariate increments, corresponding to linear changes in the simplex, are indexed by a direction vector and a signed intensity parameter inc_size and are specific to a given observation. Two cases are illustrated below with a direction pointing to a vertex of the simplex and a general direction. For the vertex direction, the inc_rate is related to the inc_size parameter and measures the relative change of the share corresponding to this vertex.

Infinitesimal increment: direction pointing to a vertex

The direction pointing to a vertex corresponds to the increments considered by Muller et al. (2018). For example, we can measure the change caused by increasing the HIGH share of the TEMPERATURES variable by \(5\%\), assuming that the ratio between the other two components remains constant, using the function VariationTable().

VariationTable(
  fit_X_compo,
  obs      =  1,             # indicator of the observation (1 is default)
  Xvar     = "TEMPERATURES", # covariate for which the impact is computed
  Xdir     = 'HIGH',         # vertex in the covariate simplex 
  inc_rate = 0.05)           # signed intensity

##                           YIELD
## Initial value       3.924848006
## New value           3.919636938
## Semi elasticity    -0.031274742
## Variation in %     -0.132771206
## Variation in units -0.005211068

The interpretation of this result is as follows: a \(5\%\) change of the HIGH share assuming the ratio between the LOW and the MEDIUM share remains constant will result in a \(-0.0052\) unit change in YIELD.

Infinitesimal increment: general direction

Let us now consider changing the covariate in the direction \((0.2,0.55,0.25)\), with an increment size of \(0.05\). Note that this direction vector will be normalized before being used within the function, and will later be given as output in attributes.

fit_X_compo.varTab <- VariationTable(
  fit_X_compo,
  obs      = 10,               # indicator of the observation
  Xvar     = "TEMPERATURES",   # covariate for which the impact is computed
  Xdir     = c(0.2,0.55,0.25), # general direction in the covariate simplex
  inc_size = 0.05)             # signed intensity

fit_X_compo.varTab

##                          YIELD
## Initial value      4.010224763
## New value          4.015157689
## Semi elasticity    0.024601746
## Variation in %     0.123008728
## Variation in units 0.004932926

attributes(fit_X_compo.varTab)

## $names
## [1] "YIELD"
## 
## $class
## [1] "data.frame"
## 
## $row.names
## [1] "Initial value"      "New value"          "Semi elasticity"   
## [4] "Variation in %"     "Variation in units"
## 
## $`X(0)`
##               LOW            MEDIUM              HIGH 
## "0.0000002999999" "0.9506845561646" "0.0493151438356" 
## attr(,"class")
## [1] "acomp"
## 
## $`X(h)`
## [1] 0.0000002805874 0.9531436237124 0.0468560957002
## 
## $Xdir
## [1] 0.1616218 0.6208904 0.2174878
## 
## $inc_size
## [1] 0.05
## 
## $inc_rates
## [1] -0.064708144  0.002586628 -0.049863955

The move between the temperature share vector of \((0.0000002999999, 0.9506845561646, 0.0493151438356)\) to \((0.0000002805874, 0.9531436237124, 0.0468560957002)\) results in an increase of the YIELD by \(0.004932926\) units. Note that the Aitchison distance between these two points is equal to the increment size \(0.05\).

Composition on scalar regression

This case is illustrated using an example from Morais et al. (2018) studying the impact of some socio-economic variables on the market shares in each of the five market segments A, B, C, D and E.

Car market data

This dataset shows monthly data on the French automobile market between 2003 and 2015. The market is divided into 5 main segments (SEG_A to SEG_E), according to the size of the vehicle chassis. Apart from data on market shares, we have four classical variables, such as HOUSEHOLD_EXPENDITURE, gross domestic product (GDP), the average national price of diesel fuel (GAS_PRICE), and SCRAPPING_SUBSIDY. We also have the DATE, generally the beginning of each month in which the sale has taken place.

summary(car_market)

##       DATE                SEG_A             SEG_B            SEG_C       
##  Min.   :2003-01-01   Min.   :0.05178   Min.   :0.3051   Min.   :0.2959  
##  1st Qu.:2006-02-22   1st Qu.:0.06979   1st Qu.:0.3721   1st Qu.:0.3398  
##  Median :2009-04-16   Median :0.07841   Median :0.3909   Median :0.3593  
##  Mean   :2009-04-16   Mean   :0.08737   Mean   :0.3910   Mean   :0.3654  
##  3rd Qu.:2012-06-08   3rd Qu.:0.09893   3rd Qu.:0.4125   3rd Qu.:0.3883  
##  Max.   :2015-08-01   Max.   :0.16036   Max.   :0.4576   Max.   :0.4484  
##      SEG_D             SEG_E              GDP         HOUSEHOLD_EXPENDITURE
##  Min.   :0.06481   Min.   :0.01845   Min.   :134773   Min.   :71647        
##  1st Qu.:0.09159   1st Qu.:0.02596   1st Qu.:151629   1st Qu.:81181        
##  Median :0.10665   Median :0.03619   Median :164700   Median :88666        
##  Mean   :0.11257   Mean   :0.04362   Mean   :162472   Mean   :86882        
##  3rd Qu.:0.13434   3rd Qu.:0.06109   3rd Qu.:173575   3rd Qu.:93219        
##  Max.   :0.18964   Max.   :0.10123   Max.   :182620   Max.   :96548        
##    GAS_PRICE     SCRAPPING_SUBSIDY
##  Min.   :0.755   Min.   :0.0000   
##  1st Qu.:1.019   1st Qu.:0.0000   
##  Median :1.125   Median :0.0000   
##  Mean   :1.140   Mean   :0.1645   
##  3rd Qu.:1.317   3rd Qu.:0.0000   
##  Max.   :1.445   Max.   :1.0000

opar <- par(mar=c(5.1, 4.1, 4.1, 8.1), xpd=TRUE)
plot(x = car_market$DATE, y = car_market$SEG_A,type = "l", col = "red",
     main = "French vehicles market shares from 2003 to 2015", 
     xlab = "DATE", ylab = "VALUE", ylim = c(0,0.5))
lines(x = car_market$DATE, y = car_market$SEG_B,type = "l", col = "blue" )
lines(x = car_market$DATE, y = car_market$SEG_C,type = "l", col = "green")
lines(x = car_market$DATE, y = car_market$SEG_D,type = "l", col = "orange")
lines(x = car_market$DATE, y = car_market$SEG_E,type = "l", col = "black")
legend("topright",
       legend = paste0("Segment ", LETTERS[1:5]),
       col = c("red", "blue", "green", "orange", "black"),
       lty = 1,
       inset=c(-0.35,0))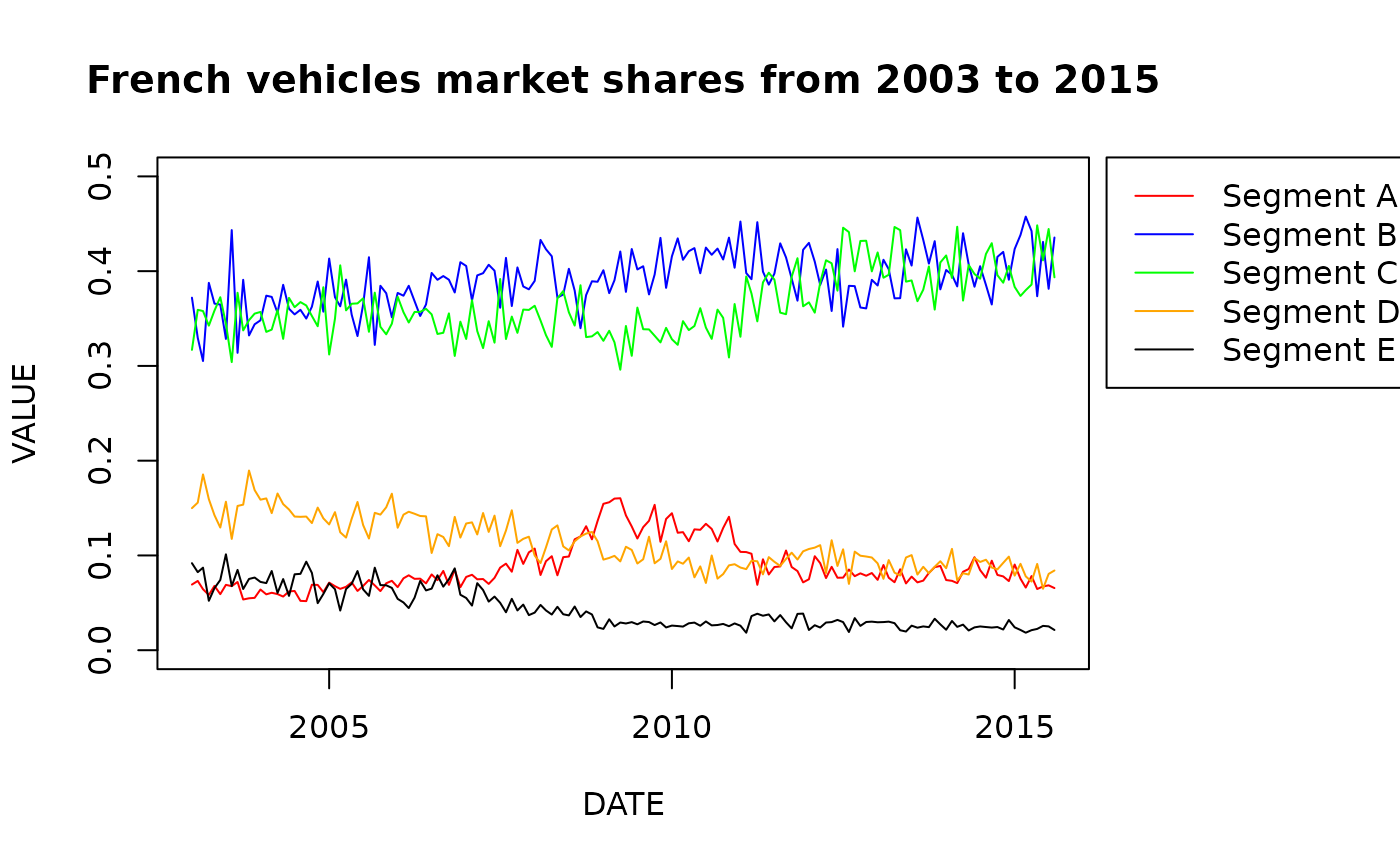

par(opar)

Regression step

We directly use the lmCoDa() function to fit a regression model explaining the market shares as a function of household expenditure, GDP, gas price and an indicator of the scrapping incentive period. As previously, the compositional variable must be included as a matrix.

car_market$SEG <- as.matrix(car_market[,c("SEG_A","SEG_B","SEG_C","SEG_D","SEG_E")])

Below we transform the response by an ilr, using the ilr() function of the compositions package.

fit_Y_compo <- lmCoDa(
  ilr(SEG) ~ HOUSEHOLD_EXPENDITURE + GDP + GAS_PRICE + SCRAPPING_SUBSIDY,
  data=car_market)

coef

The estimated coefficients are retrieved using the coef() function.

coef(fit_Y_compo, space = "simplex")  # coefficients in the simplex

##                            SEG_A      SEG_B     SEG_C     SEG_D     SEG_E
## (Intercept)           0.00510613 0.02979117 0.0299574 0.1738140 0.7613313
## HOUSEHOLD_EXPENDITURE 0.20004025 0.20000871 0.2000042 0.1999921 0.1999548
## GDP                   0.19998123 0.19999792 0.2000000 0.2000025 0.2000184
## GAS_PRICE             0.13249844 0.12769598 0.1583048 0.1951823 0.3863185
## SCRAPPING_SUBSIDY     0.25071823 0.19046324 0.1729588 0.1825495 0.2033102

coef(fit_Y_compo)                     # ... in ilr space

##                            ilr(SEG)1      ilr(SEG)2      ilr(SEG)3
## (Intercept)            1.24717388192  0.72459957006  2.03502320226
## HOUSEHOLD_EXPENDITURE -0.00011150825 -0.00008293645 -0.00011093018
## GDP                    0.00005900412  0.00004246356  0.00004089033
## GAS_PRICE             -0.02610541082  0.16036864757  0.29475342664
## SCRAPPING_SUBSIDY     -0.19436277707 -0.19093033990 -0.08827046806
##                           ilr(SEG)4
## (Intercept)            2.8974651795
## HOUSEHOLD_EXPENDITURE -0.0002527637
## GDP                    0.0001027078
## GAS_PRICE              0.8389659267
## SCRAPPING_SUBSIDY      0.0279658835

fitted

For models with compositional response the fitted() also has a space argument allowing to retrieve the fitted values in coordinate space, clr space or in the simplex.

head(fitted(fit_Y_compo, space = "simplex"))  # coefficients in the simplex

##   SEG_A        SEG_B       SEG_C       SEG_D       SEG_E       
## 1 "0.06550853" "0.3518854" "0.3312294" "0.1636691" "0.08770752"
## 2 "0.06506734" "0.3490900" "0.3309363" "0.1646582" "0.09024814"
## 3 "0.06450031" "0.3455116" "0.3305134" "0.1659005" "0.09357414"
## 4 "0.06266230" "0.3512741" "0.3315112" "0.1640017" "0.09055064"
## 5 "0.06327936" "0.3553624" "0.3319284" "0.1625658" "0.08686404"
## 6 "0.06335595" "0.3558713" "0.3319754" "0.1623847" "0.08641256"
## attr(,"class")
## [1] "acomp"

head(fitted(fit_Y_compo, space = "clr"))      # ... in clr space

##        SEG_A     SEG_B     SEG_C      SEG_D      SEG_E
## 1 -0.9018499 0.7792754 0.7187808 0.01381641 -0.6100227
## 2 -0.9123999 0.7675070 0.7141032 0.01604937 -0.5852597
## 3 -0.9258272 0.7525292 0.7081499 0.01889132 -0.5537431
## 4 -0.9439949 0.7798119 0.7219066 0.01812205 -0.5758457
## 5 -0.9286494 0.7969295 0.7287105 0.01487411 -0.6118646
## 6 -0.9267313 0.7990692 0.7295609 0.01446811 -0.6163670

head(fitted(fit_Y_compo))                     # ... in ilr space (as in the estimation)

##       [,1]      [,2]       [,3]       [,4]
## 1 1.188735 0.6369230 -0.1601446 -0.6820261
## 2 1.187874 0.6422151 -0.1504177 -0.6543402
## 3 1.186777 0.6489506 -0.1380381 -0.6191037
## 4 1.218916 0.6564617 -0.1453068 -0.6438151
## 5 1.220169 0.6487640 -0.1594550 -0.6840855
## 6 1.220325 0.6478018 -0.1612235 -0.6891192
## attr(,"class")
## [1] "rmult"

resid

The same functionality is available for the residuals.

head(resid(fit_Y_compo, space = "simplex"))  # coefficients in the simplex

##   SEG_A       SEG_B       SEG_C       SEG_D       SEG_E      
## 1 "0.2100350" "0.2099886" "0.1900386" "0.1819359" "0.2080019"
## 2 "0.2241523" "0.1884051" "0.2165972" "0.1887411" "0.1821043"
## 3 "0.1990092" "0.1761677" "0.2160209" "0.2230781" "0.1857242"
## 4 "0.2015812" "0.2391805" "0.2238778" "0.2106168" "0.1247437"
## 5 "0.2229353" "0.2138702" "0.2243390" "0.1821381" "0.1567175"
## 6 "0.1971703" "0.2164442" "0.2369534" "0.1682997" "0.1811324"
## attr(,"class")
## [1] "acomp"

head(resid(fit_Y_compo, space = "clr"))      # ... in clr space

##          SEG_A       SEG_B       SEG_C       SEG_D       SEG_E
## 1  0.050722716  0.05050182 -0.04932391 -0.09289665  0.04099603
## 2  0.117542428 -0.05618878  0.08325649 -0.05440689 -0.09020325
## 3 -0.001038231 -0.12295300  0.08098568  0.11313241 -0.07012686
## 4  0.032029651  0.20305589  0.13693794  0.07587790 -0.44790138
## 5  0.117957913  0.07644556  0.12423438 -0.08415879 -0.23447906
## 6 -0.006779935  0.08648514  0.17701586 -0.16510139 -0.09161968

head(resid(fit_Y_compo))                     # ... in ilr space (as in the estimation)

##            [,1]        [,2]        [,3]        [,4]
## 1 -0.0001561993 -0.08159755 -0.09543328  0.04583496
## 2 -0.1228465125  0.04293111 -0.08886310 -0.10085030
## 3 -0.0862067605  0.11674374  0.11039017 -0.07840421
## 4  0.1209338141  0.01583609 -0.04168174 -0.50076897
## 5 -0.0293536636  0.02207206 -0.16486648 -0.26215556
## 6  0.0659483699  0.11199333 -0.21709099 -0.10243392
## attr(,"class")
## [1] "rmult"

Interpretation tools

Finite increments interpretation

Interpretation with ilr coordinates

Finite increments interpretation as in Muller et al. (2018) can be obtained using coordinate space outputs.

coef(fit_Y_compo)

##                            ilr(SEG)1      ilr(SEG)2      ilr(SEG)3
## (Intercept)            1.24717388192  0.72459957006  2.03502320226
## HOUSEHOLD_EXPENDITURE -0.00011150825 -0.00008293645 -0.00011093018
## GDP                    0.00005900412  0.00004246356  0.00004089033
## GAS_PRICE             -0.02610541082  0.16036864757  0.29475342664
## SCRAPPING_SUBSIDY     -0.19436277707 -0.19093033990 -0.08827046806
##                           ilr(SEG)4
## (Intercept)            2.8974651795
## HOUSEHOLD_EXPENDITURE -0.0002527637
## GDP                    0.0001027078
## GAS_PRICE              0.8389659267
## SCRAPPING_SUBSIDY      0.0279658835

Following Muller et al. (2018), using the default contrast matrix below, we can interpret the impact of an additive change in the household expenditure variable on the ratio between segment E and the geometric mean of the other segments.

ilrBase(D = 5) # default contrast matrix

##         [,1]       [,2]       [,3]       [,4]
## 1 -0.7071068 -0.4082483 -0.2886751 -0.2236068
## 2  0.7071068 -0.4082483 -0.2886751 -0.2236068
## 3  0.0000000  0.8164966 -0.2886751 -0.2236068
## 4  0.0000000  0.0000000  0.8660254 -0.2236068
## 5  0.0000000  0.0000000  0.0000000  0.8944272

If the household expenditure, expressed in chain-linked prices of the previous year, increases by \(250\) million euros, approximately one percent of its range, the ratio between segment E and the geometric mean of the other segments is multiplied by \(\exp((-0.0025) * 250/0.89)\sim 0.49,\) hence approximately divided by two. However, it is difficult to describe the simultaneous changes in the ratio between the other segments with this approach.

Variation scenario in real space

In this part, we are interested in presenting on a graph the variations of the fitted shares corresponding to a change scenario of the variable “HOUSEHOLD_EXPENDITURE”. In this case, since the variable to be changed is scalar, the scenario of change is just a regular grid of values defined by a step size, a number of steps and an initial observation. The first step VariationScenario() creates the grid for the covariate (\(X\)) and computes the corresponding fitted values (\(Y\)).

vs_exp2 <- VariationScenario(
  fit_Y_compo,
  Xvar = "HOUSEHOLD_EXPENDITURE",
  obs = 1,
  inc_size = 100,
  n_steps = 150,
  add_opposite = TRUE)

plot(x = vs_exp2$HOUSEHOLD_EXPENDITURE, y = vs_exp2$Y[,1],type = "l", col = "red",
     main = "Variation scenario of houshold expenditure for observation 1",
     xlab = "Household expenditure", ylab = "Market share of segment")
lines(x = vs_exp2$HOUSEHOLD_EXPENDITURE, y = vs_exp2$Y[,2],type = "l", col = "blue" )
lines(x = vs_exp2$HOUSEHOLD_EXPENDITURE, y = vs_exp2$Y[,3],type = "l", col = "green")
lines(x = vs_exp2$HOUSEHOLD_EXPENDITURE, y = vs_exp2$Y[,4],type = "l", col = "orange")
lines(x = vs_exp2$HOUSEHOLD_EXPENDITURE, y = vs_exp2$Y[,5],type = "l", col = "black")
legend("topleft",
       legend = paste0("SEG_", LETTERS[1:5]),
       col = c("red", "blue", "green", "orange", "black"),
       lty = 1)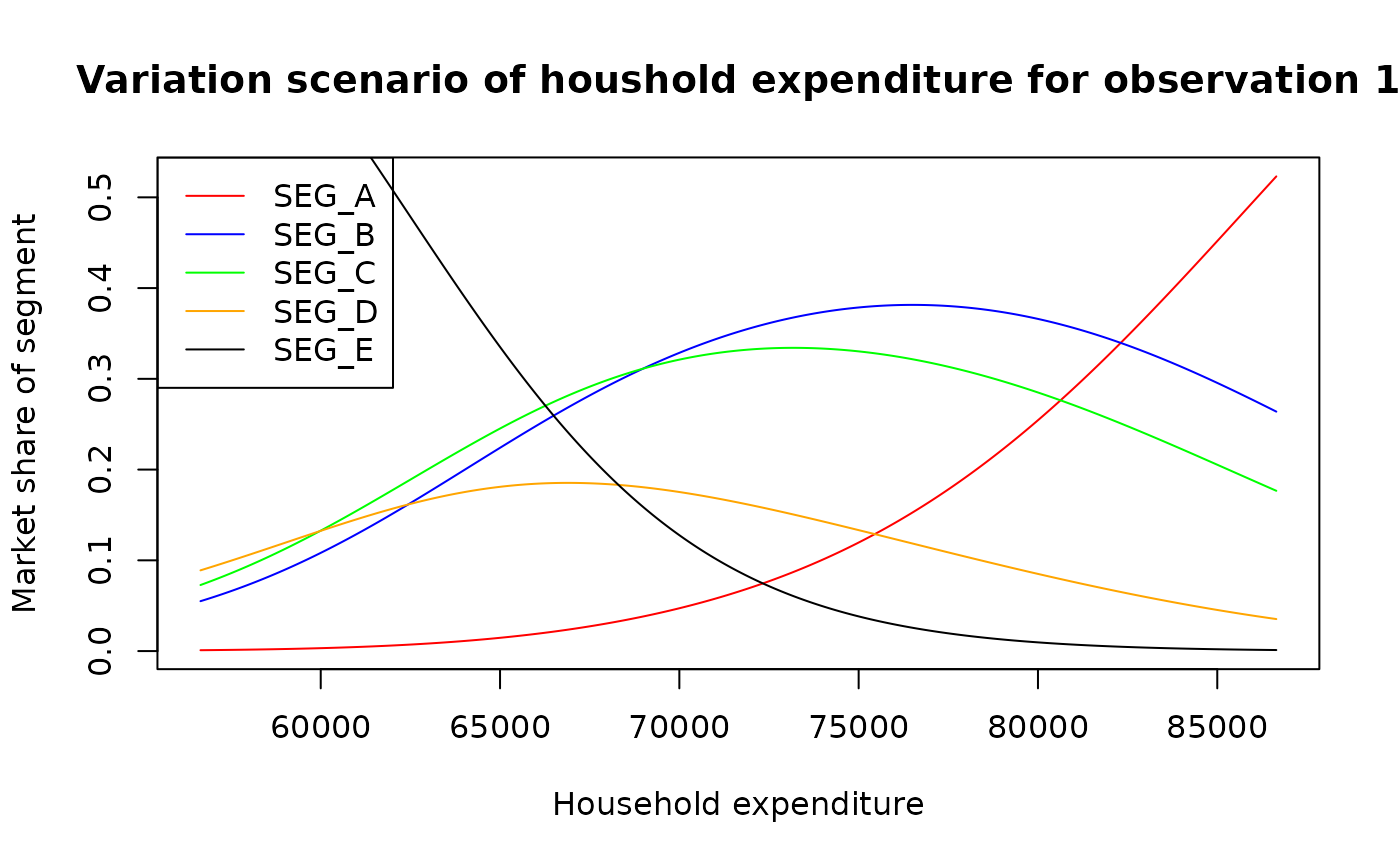

Infinitesimal increments interpretation

Semi-elasticities

The use of semi-elasticities for the interpretation of compositional covariates is described in Morais and Thomas-Agnan (2021). The only difference with the previous section is that it involves derivatives of the logarithm of the \(Y\) components with respect to \(X\), in contrast with derivatives of \(Y\) with respect to the logarithm of the components of \(X\). The Impacts() function computes these elasticities.

Impacts(fit_Y_compo,
        Xvar = "HOUSEHOLD_EXPENDITURE",
        obs=4)

##                              SEG_A         SEG_B         SEG_C          SEG_D
## HOUSEHOLD_EXPENDITURE 0.0001933935 0.00003569699 0.00001296924 -0.00004740457
##                               SEG_E
## HOUSEHOLD_EXPENDITURE -0.0002339346
## attr(,"obs")
## [1] 4

The semi-elasticities are then used for evaluating the impact on \(Y\) of an infinitesimal additive change of any of the scalar explanatory variables.

Infinitesimal Increments approach

For example, we can measure the change caused by an increase of \(2500\) million euros in HOUSEHOLD_EXPENDITURE using the function VariationTable().

fit_Y_compo.VarTab <- VariationTable(
  fit_Y_compo,                      # model output
  Xvar = "HOUSEHOLD_EXPENDITURE",   # variable to be changed
  inc_size = 2500,                  # additive increment of X
  obs = 1)                          # observation index

fit_Y_compo.VarTab

##                              SEG_A         SEG_B         SEG_C           SEG_D
## Initial parts          0.065508533 0.35188544895 0.33122939357   0.16366910523
## New parts              0.096976210 0.38218939438 0.34093421621   0.14376119345
## Semi elasticity        0.000192144 0.00003444751 0.00001171976  -0.00004865405
## Variation in %        48.035998361 8.61187796119 2.92994004579 -12.16351231860
## Variation in % points  3.146767770 3.03039454268 0.97048226455  -1.99079117759
##                                SEG_E
## Initial parts           0.0877075195
## New parts               0.0361389855
## Semi elasticity        -0.0002351841
## Variation in %        -58.7960237233
## Variation in % points  -5.1568533997

For the first month, an increase of \(2500\) million euros of total HOUSEHOLD_EXPENDITURE will result in a decrease of 2 percentage points in the “SEG_D” share, and an increase of 3 percentage points in the “SEG_B” share. We can visualize these changes more globally with a barplot.

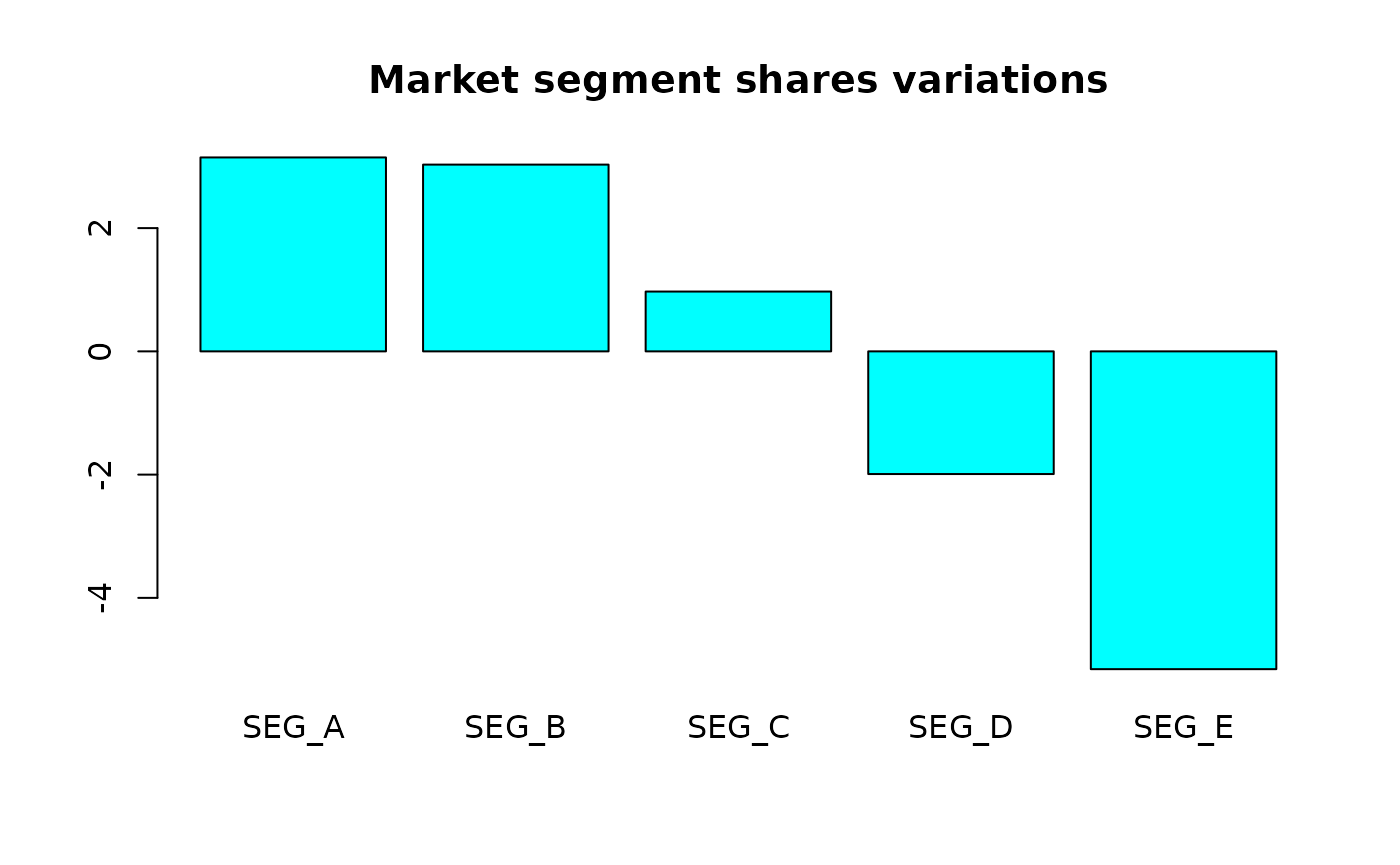
barplot(as.matrix(fit_Y_compo.VarTab[5,]),col = "cyan")
title("Market segment shares variations")

Composition on composition regression

This case is illustrated using an example from Nguyen et. al (2020) studying the impact of some socio-economic variables on the outcome of French departmental elections in 2015.

Election data

This dataset contains the vote shares for 3 groups of parties (left, right, extreme_right) in different departments of France in the 2015 French departmental election for 95 departments in France. The election results originate from the French ‘Ministry of the Interior’. The corresponding socio-economic data (for 2014) have been downloaded from the INSEE website. The regression involves the following explanatory variables:

four scalar variables: the unemployment rate (unemp_rate), the proportion of people who own assets (asset_owner_rate), the proportion of people who pay income tax (income_taxpayer_rate), the proportion of foreigners (forgeigner_rate).
two compositional variables:
- the Age variable has three levels: Age_1839 for people from 18 to 39 years old, Age_4064 for people from 40 to 64 years old, and Age_65plus for people over 65.
- Diploma has three levels: Educ_BeforeHighschool for people with at most some secondary education, Educ_Highschool for people with at least secondary education and at most a high school diploma, and Educ_Higher for people with a university diploma.

data("election")
summary(election[1:3])

##       left            right        extreme_right    
##  Min.   :0.1740   Min.   :0.1195   Min.   :0.05563  
##  1st Qu.:0.3108   1st Qu.:0.3296   1st Qu.:0.19956  
##  Median :0.3598   Median :0.3760   Median :0.26102  
##  Mean   :0.3682   Mean   :0.3841   Mean   :0.24777  
##  3rd Qu.:0.4322   3rd Qu.:0.4421   3rd Qu.:0.30400  
##  Max.   :0.7228   Max.   :0.6367   Max.   :0.41485

summary(election[4:6])

##     Age_1839         Age_4064        Age_65plus    
##  Min.   :0.2270   Min.   :0.3836   Min.   :0.1536  
##  1st Qu.:0.2756   1st Qu.:0.4208   1st Qu.:0.2243  
##  Median :0.3077   Median :0.4315   Median :0.2613  
##  Mean   :0.3140   Mean   :0.4295   Mean   :0.2566  
##  3rd Qu.:0.3486   3rd Qu.:0.4384   3rd Qu.:0.2872  
##  Max.   :0.4320   Max.   :0.4511   Max.   :0.3364

summary(election[7:9])

##  Educ_BeforeHighschool Educ_Highschool   Educ_Higher    
##  Min.   :0.3484        Min.   :0.1444   Min.   :0.1617  
##  1st Qu.:0.5613        1st Qu.:0.1596   1st Qu.:0.2034  
##  Median :0.5918        Median :0.1677   Median :0.2324  
##  Mean   :0.5889        Mean   :0.1689   Mean   :0.2422  
##  3rd Qu.:0.6349        3rd Qu.:0.1780   3rd Qu.:0.2670  
##  Max.   :0.6867        Max.   :0.2234   Max.   :0.4998

summary(election[10:13])

##    unemp_rate      asset_owner_rate income_taxpayer_rate forgeigner_rate  
##  Min.   :0.08353   Min.   :0.3998   Min.   :0.4499       Min.   :0.01342  
##  1st Qu.:0.10513   1st Qu.:0.5894   1st Qu.:0.5143       1st Qu.:0.02994  
##  Median :0.11648   Median :0.6189   Median :0.5432       Median :0.04436  
##  Mean   :0.11731   Mean   :0.6158   Mean   :0.5525       Mean   :0.05049  
##  3rd Qu.:0.12423   3rd Qu.:0.6645   3rd Qu.:0.5777       3rd Qu.:0.05886  
##  Max.   :0.16246   Max.   :0.7229   Max.   :0.7452       Max.   :0.22824

Regression step

First, we must ensure that all compositional variables are stored as a matrix.

election$VOTE <- as.matrix(election[,c("left","right","extreme_right")])
election$AGE  <- as.matrix(election[,c("Age_1839","Age_4064","Age_65plus")])
election$EDUC <- as.matrix(election[,c("Educ_BeforeHighschool","Educ_Highschool","Educ_Higher")])

The next step consists of applying a log-ratio transformation (alr or ilr) to the compositional variables and then using the “lm” function to perform regression in coordinates space. In this example, the response variable, VOTE, is transformed by an ilr, the variable Age is transformed by an alr, and EDUC is transformed by an ilr.

fit_YX_compo <- lmCoDa(
  ilr(VOTE) ~
  alr(AGE) + unemp_rate + asset_owner_rate +
  ilr(EDUC) + income_taxpayer_rate + forgeigner_rate,
  data = election)

With the coef() function we can access the estimated coefficients in coordinate space, as well as in the simplex:

coef(fit_YX_compo)

##                       ilr(VOTE)1 ilr(VOTE)2
## (Intercept)          -0.07020983 -6.9109264
## alr(AGE)Age_1839     -0.10463431  0.5592385
## alr(AGE)Age_4064      0.23336593 -0.2278400
## unemp_rate           -8.16701488 17.2562747
## asset_owner_rate     -2.96545832  2.8971115
## ilr(EDUC)1           -1.21486657 -2.2816886
## ilr(EDUC)2           -0.76776003  0.9077666
## income_taxpayer_rate  2.91875389  1.7559045
## forgeigner_rate      -1.45607088 -0.5496067

coef(fit_YX_compo, space = "simplex")

##                                   left                right extreme_right
## (Intercept)            0.5247472819482  0.47514740845404074  0.0001053096
## Age_1839              -0.1543205229982 -0.30229578360147996  0.4566163066
## Age_4064              -0.0719993474717  0.25802991714545126 -0.1860305697
## Age_65plus             0.2263198704699  0.04426586645602869 -0.2705857369
## unemp_rate             0.0000002135099  0.00000000000205759  0.9999997865
## asset_owner_rate       0.1892554610820  0.00285566966007836  0.8078888693
## Educ_BeforeHighschool -1.3364388553996  0.32169418104455588  1.0147446744
## Educ_Highschool        1.1957612695548  0.42416115809884591 -1.6199224277
## Educ_Higher            0.1406775858448 -0.74585533914340196  0.6051777533
## income_taxpayer_rate   0.0076516015515  0.47468732197433899  0.5176610765
## forgeigner_rate        0.7635086355050  0.09739055674009536  0.1391008078

Standard errors and confidence intervals are provided for the clr of parameters by the function confint(). The following example is for the case of the compositional explanatory variable AGE.

confint(fit_YX_compo, parm = "AGE")

##               Y          X         EST        SD      2.5 %     97.5 %
## 1          left   Age_1839 -0.15432052 0.4909885 -1.1303733 0.82173229
## 2         right   Age_1839 -0.30229578 0.3747233 -1.0472210 0.44262946
## 3 extreme_right   Age_1839  0.45661631 0.3953292 -0.3292722 1.24250484
## 4          left   Age_4064 -0.07199935 0.6721951 -1.4082790 1.26428030
## 5         right   Age_4064  0.25802992 0.5130205 -0.7618211 1.27788092
## 6 extreme_right   Age_4064 -0.18603057 0.5412314 -1.2619630 0.88990183
## 7          left Age_65plus  0.22631987 0.1919484 -0.1552609 0.60790069
## 8         right Age_65plus  0.04426587 0.1464954 -0.2469573 0.33548902
## 9 extreme_right Age_65plus -0.27058574 0.1545511 -0.5778232 0.03665172

When providing the argument y_ref the function returns the same information for the differences of clr parameter values, which coincide with differences in elasticities (Dargel and Thomas-Agnan 2024).

confint(fit_YX_compo, parm = "AGE", y_ref = "left")

##   Y_ref             Y          X       DIFF        SD      2.5 %    97.5 %
## 1  left          left   Age_1839  0.0000000 0.0000000  0.0000000 0.0000000
## 2  left         right   Age_1839 -0.1479753 0.7789026 -1.6963824 1.4004319
## 3  left extreme_right   Age_1839  0.6109368 0.8088834 -0.9970701 2.2189437
## 4  left          left   Age_4064  0.0000000 0.0000000  0.0000000 0.0000000
## 5  left         right   Age_4064  0.3300293 1.0663682 -1.7898406 2.4498991
## 6  left extreme_right   Age_4064 -0.1140312 1.1074138 -2.3154970 2.0874346
## 7  left          left Age_65plus  0.0000000 0.0000000  0.0000000 0.0000000
## 8  left         right Age_65plus -0.1820540 0.3045064 -0.7873926 0.4232846
## 9  left extreme_right Age_65plus -0.4969056 0.3162271 -1.1255443 0.1317331

The following example is for the case of the scalar explanatory variable unemp_rate.

confint(fit_YX_compo, parm = "unemp_rate")

##               Y          X        EST       SD      2.5 %    97.5 %
## 1          left unemp_rate  -1.269893 2.465914  -6.171968  3.632182
## 2         right unemp_rate -12.819796 1.881990 -16.561068 -9.078524
## 3 extreme_right unemp_rate  14.089689 1.985480  10.142685 18.036693

In this case the difference in clr parameters coincides with a semi-elasticities difference.

confint(fit_YX_compo, parm = "unemp_rate", y_ref = "left")

##   Y_ref             Y          X      DIFF       SD      2.5 %    97.5 %
## 1  left          left unemp_rate   0.00000 0.000000   0.000000  0.000000
## 2  left         right unemp_rate -11.54990 3.911918 -19.326539 -3.773267
## 3  left extreme_right unemp_rate  15.35958 4.062492   7.283616 23.435549

Fitted values and residuals, both in the simplex space, can be accessed directly using fitted, and residuals functions as shown previously.

Interpretation tools

Finite increments

Interpretation with ilr coordinates

Finite increments interpretation as in Muller et al. (2018) can be obtained using coordinate space outputs, but this time we need to consider two contrast matrices, one for the response and one for the explanatory composition. In the present model, the VOTE and the EDUC compositions are both ilr transformed with the default contrast matrix.

ilrBase(D = 3)

##         [,1]       [,2]
## 1 -0.7071068 -0.4082483
## 2  0.7071068 -0.4082483
## 3  0.0000000  0.8164966

This means we can interpret the element in the last row and last column of the corresponding parameter matrix that is expressed using the ilr spaces of both the response VOTE and the “EDUC” variables (whose contrast matrices coincide in our example).

coef(fit_YX_compo, split = TRUE)[["ilr(EDUC)"]]

##            ilr(VOTE)1 ilr(VOTE)2
## ilr(EDUC)1  -1.214867 -2.2816886
## ilr(EDUC)2  -0.767760  0.9077666

The value of about \(0.90777\) indicates that an additive unit increase in the second ilr coordinate of the explanatory EDUC composition leads to an additive increase of the second ilr coordinate of the response VOTE composition. Given the form of the contrast matrix, these ilr coordinates can be interpreted as principal balances of the last component against the first two in both compositions. The above change in education corresponds to a move in the direction of the high education vertex in the simplex. Therefore, a multiplication of the ratio between the higher education level to the geometric mean of the other two by \(\exp(1/081) \sim 3.43\) induces a multiplication of the ratio of the vote share for the extreme right party to the geometric mean of the other two parties by \(\exp(0.91/081)\sim 3.07.\) If one wishes to evaluate the impact of this change on other ratios of \(Y\) it would mean changing the contrast matrix of the response. Similarly, if one wishes to evaluate the impact of changing the education composition in the direction of the other two vertices, it would mean changing the \(X\) contrast matrix.

VariationScenario

As in the case of scalar on composition regression, to evaluate the impact of a given compositional covariate, we create scenarios of changes in its simplex space described by a linear equation \(x(h)=x(0)\oplus h\odot u,\) where \(x(0)\) is the initial point, \(h\) is the signed-intensity of change and \(u\) is a vector of the simplex defining the direction of change. We then compute the predicted value \(y(h)\) corresponding to \(x(h)\), keeping the other covariates at their value for the initial point.

To present the variations of \(Y\) induced by a change scenario of \(X\), we propose two plots. The first one is a graph of the shares of \(Y\) as a function of one of the shares of \(X\) and the second one presents the evolution of the other shares of \(X\). In the following illustration, we choose the direction of change joining the initial point (in this case, observation 1, Landes department) to the vertex Age_1839.

VS_election<-VariationScenario(
  fit_YX_compo,
  Xvar = "AGE",
  Xdir = "Age_1839",
  n_steps = 100,
  obs = 1)


opar <- par(mfrow = c(2,1), mar = c(5,4,1,2))
plot(x = VS_election$X[,1],  y = VS_election$Y[,1], col = "Orange",
     xlim = c(0,1), ylim = c(0,1), xlab = "% Age_1839", ylab = "% VOTE")
lines(x = VS_election$X[,1],  y = VS_election$Y[,1], lwd = 1.5, col = "orange")
lines(x = VS_election$X[,1],  y = VS_election$Y[,2], lwd = 1.5, col = "darkblue")
lines(x = VS_election$X[,1],  y = VS_election$Y[,3], lwd = 1.5, col = "red")
legend("top",
       legend = c("left", "right", "extreme_right"),
       col = c("orange", "darkblue", "red"),
       lty = 1)


plot(x = VS_election$X[,1],  y = VS_election$X[,1], col = "Orange",
     xlim = c(0,1), ylim = c(0,1), xlab = "% Age_1839", ylab = "% AGE")
lines(x = VS_election$X[,1],  y = VS_election$X[,1], lwd = 1.5, col = "orange")
lines(x = VS_election$X[,1],  y = VS_election$X[,2], lwd = 1.5, col = "darkblue")
lines(x = VS_election$X[,1],  y = VS_election$X[,3], lwd = 1.5, col = "red")
legend("top",
       legend = c("18-39","40-64", "65_plus"),
       col = c("orange", "darkblue", "red"),
       lty = 1)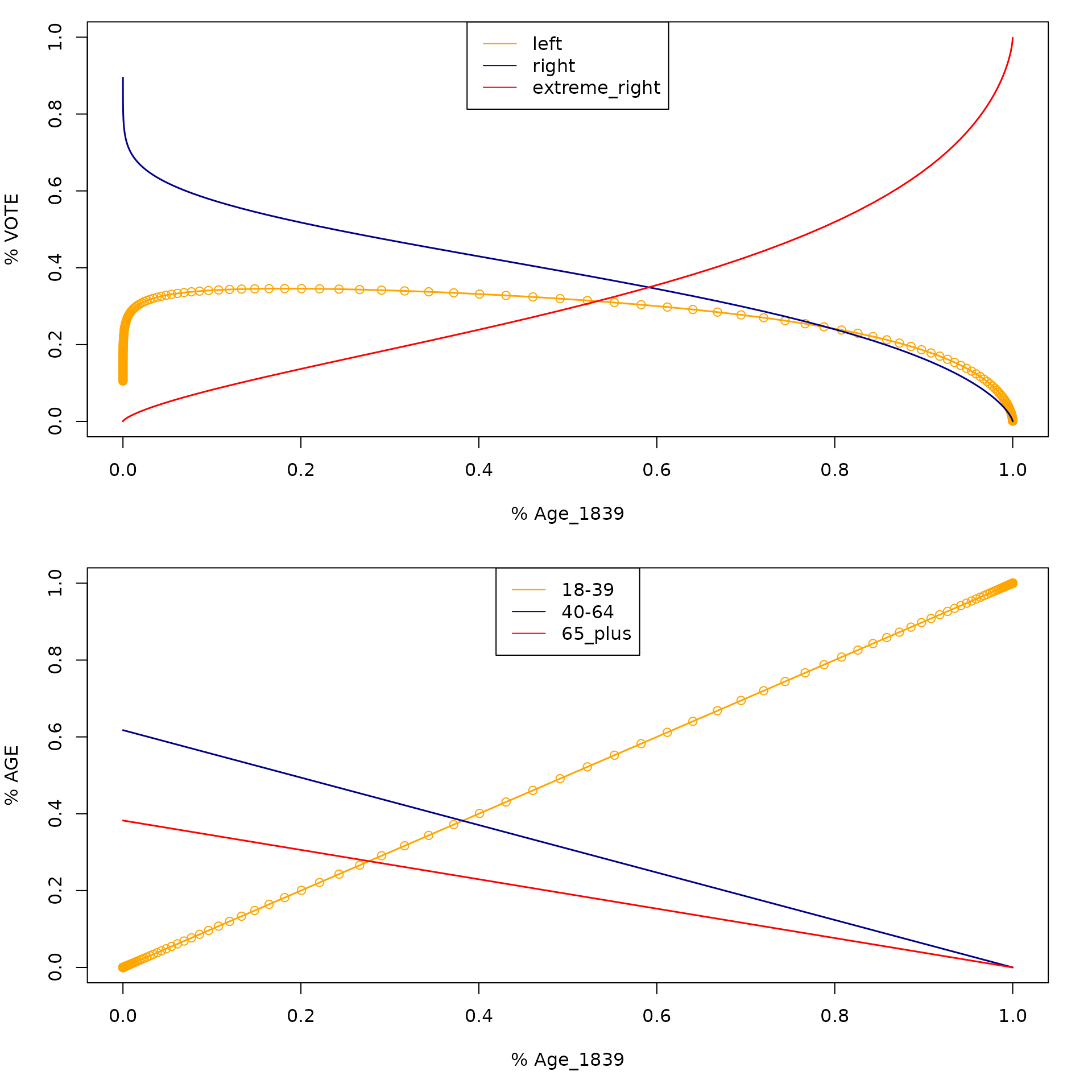

par(opar)

The vertical line corresponds to the initial department of Landes, and we can read the values of its fitted vote shares on the first graph and the values of its age characteristics on the second.
For the specified direction, the bottom graph shows that an increase in the share of voters aged between \(18\) and \(39\) years corresponds to a linear decrease in the other shares. On the top graph, we see that an increase in the share of voters aged between \(18\) and \(39\) years induces an increase in the share of the extreme right, a decrease in the share of the right parties, and a simultaneous decrease in the left party’s share.

Infinitesimal increments

Elasticities

The function Impacts() computes elasticities (or semi-elasticities, depending on the nature of the considered covariate) of covariates for a given observation. This function takes a “lmCoDa” object as input, along with the covariate’s name and the index of the observation.

Impacts(fit_YX_compo, Xvar = 'AGE', obs = 3)

##                  left      right extreme_right
## Age_1839   -0.1279812 -0.2759565     0.4829556
## Age_4064   -0.1051949  0.2248344    -0.2192261
## Age_65plus  0.2331761  0.0511221    -0.2637295
## attr(,"obs")
## [1] 3

The semi-elasticities are then used for evaluating the impact on \(Y\) of an infinitesimal additive change of any of the scalar explanatory variables.

Increments approach

Infinitesimal increment: direction pointing to a vertex

For example, we can measure the change caused by increasing the Higher share of the EDUC variable by 5%, assuming that the ratio between the other two components remains constant, using the function VariationTable(). Assuming that the voting population for the first department is \(100\;000\) individuals (we do not have this information in the dataset). The total of the response must be specified by the user in case he wants to know the variation in units.

VariationTable(
  fit_YX_compo,
  Xvar = "AGE",
  Xdir = 'Age_1839',
  Ytotal = 100000,
  inc_rate = 0.05)

##                               left        right extreme_right
## Initial parts           0.34161097    0.4756646     0.1827245
## New parts               0.34061774    0.4693200     0.1900622
## Elasticity             -0.05051647   -0.2317484     0.6977253
## Variation in %         -0.29074696   -1.3338252     4.0157495
## Variation in % points  -0.09932235   -0.6344534     0.7337757
## Variation in units    -99.32234990 -634.4533879   733.7757378

A \(5\%\) increase in the direction of Age_1839 will result in a \(0.099\) percentage points decrease in the left share, a \(0.63\) percentage points decrease in the right proportion, and a \(0.73\) percentage points increase in the extreme_right share. In units these changes correspond respectively to a decrease of \(99\) votes for the left parties, a decrease of \(634\) votes for the right parties and an increase of \(733\) votes for the extreme_right share. It is easy to check that the sum of these changes is zero.

Infinitesimal increment: General direction

For a general direction \((0.45,0.2,0.35)\), with an increment size of \(0.1\), we get the following results.

VT <- VariationTable(
  fit_YX_compo,
  Xvar = "AGE",
  Xdir = c(0.45,0.2,0.35) ,
  inc_size=0.1,
  Ytotal = 100000)
VT

##                              left         right extreme_right
## Initial parts           0.3416110     0.4756646     0.1827245
## New parts               0.3454412     0.4630204     0.1915383
## Elasticity              0.1121240    -0.2658202     0.4823571
## Variation in %          1.1212404    -2.6582020     4.8235706
## Variation in % points   0.3830280    -1.2644125     0.8813844
## Variation in units    383.0280319 -1264.4124527   881.3844208

Note that this direction vector will be normalized before being used within the function, and will later be given as output in the table’s attributes.

attributes(VT)

## $names
## [1] "left"          "right"         "extreme_right"
## 
## $class
## [1] "data.frame"
## 
## $row.names
## [1] "Initial parts"         "New parts"             "Elasticity"           
## [4] "Variation in %"        "Variation in % points" "Variation in units"   
## 
## $`X(0)`
##    Age_1839    Age_4064  Age_65plus 
## "0.2906800" "0.4380762" "0.2712438" 
## attr(,"class")
## [1] "acomp"
## 
## $`X(h)`
## [1] 0.3116451 0.4091594 0.2791955
## 
## $Xdir
## [1] 0.5254862 0.1320255 0.3424884
## 
## $inc_size
## [1] 0.1
## 
## $inc_rates
## [1]  0.07212431 -0.06600860  0.02931571

References

Coenders, G. and Pawlowsky-Glahn, V. (2020). “On interpretations of tests and effect sizes in regression models with a compositional predictor.” SORT-Statistics and Operations Research Transactions, pages 201–220.

Dargel, L., and C. Thomas-Agnan (2024). “Pairwise share-ratio interpretations of compositional regression models.” Computational Statistics & Data Analysis, Volume 195, pages 107945

Morais, J., and C. Thomas-Agnan. (2021) “Impact of covariates in compositional models and simplicial derivatives.” Austrian Journal of Statistics 50.2 (2021): 1-15.

Muller I, Hron K, Fiserova E, Smahaj J, Cakirpaloglu P, Vancakova J (2018). “Interpretation of Compositional Regression with Application to Time Budget Analysis.” Austrian Journal of Statistics, 47(2).

Christine Thomas-Agnan

Lukas Dargel

Rodrigue Nasr

Introduction

Scalar on composition regression

Rice yield data

Regression step with the compositions package

coef

fitted

residuals

Interpretation tools

Finite increments interpretation

Interpretation with ilr coordinates

Interpretation with clr coordinates

Variation scenario in the simplex space

Infinitesimal increments interpretation

Semi-elasticities

Increments approach

Infinitesimal increment: direction pointing to a vertex

Infinitesimal increment: general direction

Composition on scalar regression

Car market data

Regression step

coef

fitted

resid

Interpretation tools

Finite increments interpretation

Interpretation with ilr coordinates

Variation scenario in real space

Infinitesimal increments interpretation

Semi-elasticities

Infinitesimal Increments approach

Composition on composition regression

Election data

Regression step

Interpretation tools

Finite increments

Interpretation with ilr coordinates

VariationScenario

Infinitesimal increments

Elasticities

Increments approach

Infinitesimal increment: direction pointing to a vertex

Infinitesimal increment: General direction

References